Systems Medicine
of Infectious Diseases
Research and Consulting Group
Machine Learning for Multiscale Analysis of Biomedical Data
A python tool to compute cell decay with a half-life in discrete-time – py_discrete_decay()
By Gustavo Hernadez-Mejia and Esteban A. Hernandez-Vargas
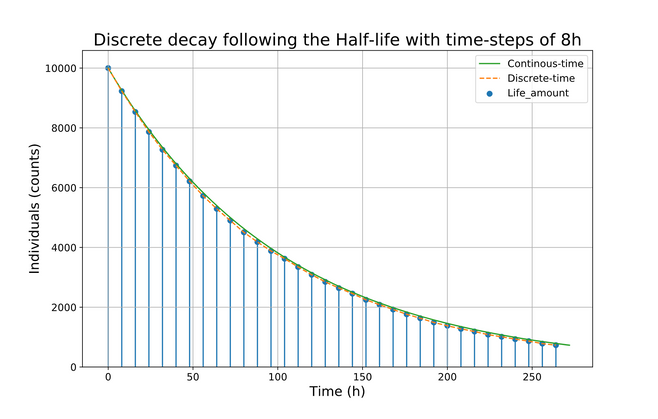
The half-life is the necessary time for a quantity (in our case cells or a set of individuals) to reduce to half its initial value1. While in continuous time, the half-life is an intuitive term, the discrete version is a bit tricky. To this end, the Tau-leaping approximate method is used2.
Given the half-life of a cell population (N) and time-step size for the decay, we set the probability of a cell to be selected. This indicates the probability to either keep or not the selected cell under a Poisson distributed random variable. The time-step can be selected as a resolution parameter, the smaller time-step the higher resolution of decay. The population is any discrete quantity. The initial population size is consistent with the "law of large numbers". The higher the initial population the better behavior of the discrete decay.
The probability of elimination (dying) is given by(code):
prob_dying = 1 - np.exp(-L * step_long), where L = np.log(2)/Half_life.
This probability is taken to select individuals to continue for the next time-step or not (live/die). On each time-step (step_long), cells or individuals are uniformly randomly selected to be eliminated. The file "Test_half_life_decay.py" sets different examples using this approach. The function is called from the file "py_funct_discrete_decay.py()".
In code form:
# Example
N=10000 # Initial population of size N
life = np.arange(N)
Half_life = 72 # 72 h (3d)
stop = 40 # 40*step_long (h)
step_long = 1
evol1, pol1 = py_discrete_decay(life, Half_life, step_long, stop)
# evol, a list containing the living individuals for each step in the decay.
# pol, an array with the number of individuals for each step in the decay.